
In equation-(2), one can see that the magnetic field increases with the increase in current through the wire and decreases with the increase in distance from the wire. To understand this, one can check the procedure of finding the magnetic field due to a current carrying straight wire by using Biot Savart law. You need to convert those into single variable by using the relations between the variables. While derivation, there may arise more than one variables. You need to familiar with the concepts of vector product too. To use this law we need to know the value of current through the wire, distance of target point where we want to find the magnetic field and the angle between the length and the distance vector. One can find magnetic field due to a current carrying wire by using the formula of Biot Savart law.
#Biot savart law how to
How to use Biot Savart law to find the Magnetic field?
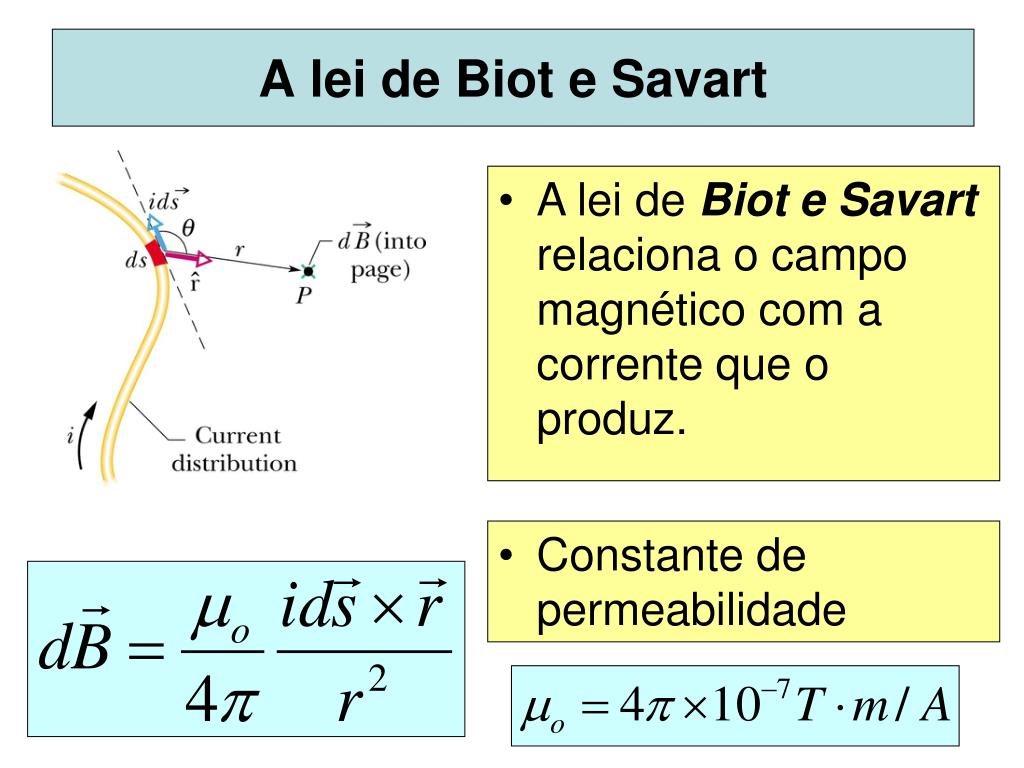

Application of Biot-Savart lawīiot Savart law is used to find the magnetic field due to a current-carrying wire. \small ………… (4)īoth of equation-(3) and (4) are the vector forms of Biot-Savart law. Then, one can get the formula of Biot-Savart law as, Formula of Biot Savart law to find magnetic field sine of the angle between the direction of elementary length and the distance vector.Īnd inversely proportional to the square of the distance ( r) of the target point from the elementary length.length of the elementary portion of the wire ( dL).Limitation of Biot Savart law Statement of Biot-Savart law of magnetismīiot Savart law of magnetostatics states that the magnetic field at a small distance from an elementary portion of a current carrying wire is.How to use the Biot Savart law to find the Magnetic field?.In this article, I’m going to explain the Biot Savart law, its statement, formula, vector form, uses and limitations. Now, how to find the magnitude or value of the magnetic field? Biot-Savart law of magnetostatics is a fundamental law that helps to find the magnitude of the magnetic field at a distance from a current carrying wire or conductor. Then we learned to find the direction of magnetic field in another article. A bar magnet, a current-carrying wire and a moving charge are the origins of magnetic field. Or, where n is the number of turns per unit length.We have discussed the origin and definition of magnetic field. If I is the current passing through the solenoid, the magnetic induction inside the solenoid is given as:

The magnetic field at the centre of a wire PQ of length l bent in a shape of a arc of radius r is:Ĭonsider a solenoid of length l and radius of cross section r ( r<< l) having N turns. Let Φ 1 and Φ 2 be the angles wich point P makes with X and Y and Φ be the angle that P makes with dl.ĬASE 3: Field due to a circular current loopĬonsider a circular loop of radius r carrying current i and having N turns.ĬASE 4: Field at the centre of a current arc To find magnetic field consider a small current element at a distance l making an angle θ as shown.Īccording to Biot Savart Law, magnetic field at point P is: Where α, β are the angles between the wire and the lines joining the end points of wire to the point A where the field is to be calculated.Ĭonsider a conductor XY carrying current I in the direction from X to Y and P be the observation point at a distance 'a' from the straight conductor. The magnetic induction at a distance r from the wire is given by: If the wire is gripped in the right hand with the thumb in direction of current the curling fingers give the direction of lines of force in circles.ĬASE 2: Field of a straight current carrying wire of finite lengthĬonsider a straight wire PQ carrying a current i as shown.

The magnetic lines of force for a long straight wire are concentric circles centred at the wire and lying in the plane perpendicular to the wire. The magnetic field due to a current carrying straight wire of infinite length at a distance r from the wire is CASE 1: Field of a straight infinite current wire


 0 kommentar(er)
0 kommentar(er)
